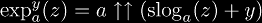This is a complete rewrite of the previous identities page. All of the series expansions have been moved to the Special Functions pages.
There are an unnecessarily large number of notations in common use for functions related to tetration. Ideally, only the most powerful notations would be used, however, as a matter of convinience we use left-superscript notation in preference to arrow notation and tower notation. Also, even though box notation is closer to hyper-operation terminology, arrow notation will be used, because it is more well-known.
 for tetration.
For more information, see the Hyperops page.
for tetration.
For more information, see the Hyperops page.
 (for hyper-roots) and
(for hyper-roots) and
 (for hyper-logs).
(for hyper-logs).
 or
or
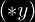 . For more information, see
Haskell sections.
. For more information, see
Haskell sections.
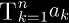
When choosing a notation, keep in mind your audience, and familiarity with tetration.
In general, tetration should be written with left-superscript notation.
If there is confusion with multiples in front, then use tower notation
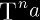 , or if there is a complicated
expression in the height, then use arrow notation
, or if there is a complicated
expression in the height, then use arrow notation
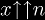 .
.
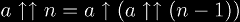
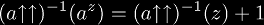
The infinite tetrate is topologically conjugate to the 2nd super-root and the Lambert W-function.
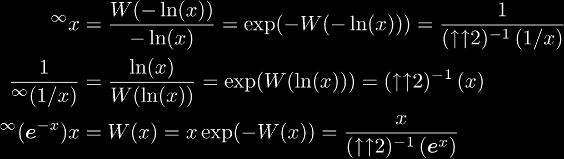
for more information see the section on topological conjugacy.
For integer values:
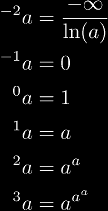
For infinite values:
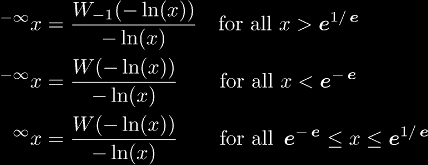
For integer values from any x:
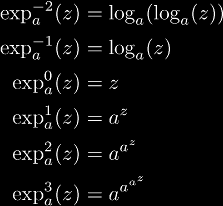
For integer values from -1:
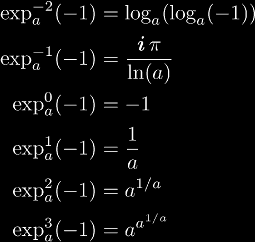
Notations for super-roots
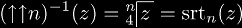
Notations for super-logs
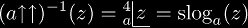
Exponentiation can be expressed in terms of exp and log:
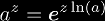
Exponentiation can be expressed in terms of tet and slog:
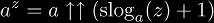
Iterated exponentials can be expressed in terms of tet and slog: