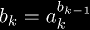Definitions

A nested exponential of height n is the solution b₁ of a recurrence equation $b_k = a_k^{b_{k-1}}$ where a_k = 1 for all k > n.
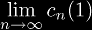An infinite exponential is the limit of solutions $\lim_{n\to\infty} c_n(1)$ of a recurrence equation 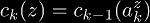$c_k(z) = c_{k-1}(a_k^z)$ where c₀(z) = z.

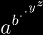
Informally, a nested exponential is an expression of the form $a^{b^{\cdot^{\cdot^{y^z}}}}$

Nested exponentials have also be called: towers, infinite exponentials, heterogeneous towers, exponential towers, n-ary exponentials, and n-ary towers. Here, we use the terms nested exponential and n-ary tower synonymously.

Notations

There are five parts to N-ary tower notation:

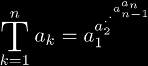
$\BigT{k=1}{n}a_k = a_1^{a_2^{\cdot^{\cdot^{a_{n-1}^{a_n}}}}}$	(Barrow's notation) for nested exponentials
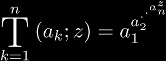
$\BigT{k=1}{n}(a_k; z) = a_1^{a_2^{\cdot^{\cdot^{a_{n}^{z}}}}}$	(Barrow-Shell notation) for nested exponential functions
$\bigT(a_1, a_2, a_3, \cdots, a_n) = a_1^{a_2^{\cdot^{\cdot^{a_{n-1}^{a_n}}}}}$	(Brunson's notation) for arbitrary nested exponentials
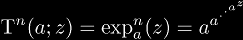
${\rm T}^n(a; z) = \exp_a^{n}(z) = a^{a^{\cdot^{\cdot^{a^z}}}}$	(similar to Galidakis' notation) for iterated exponentials
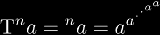
${\rm T}^na = {}^{n}a = a^{a^{\cdot^{\cdot^{a^a}}}}$	(similar to Maurer's notation) for tetration

for more notations, see the Tetration Definitions page.

One thing to note is that the last two notations can be implied by the first two, by assuming that k = 1 implicitly. So while it may seem to duplicate what can be expressed with more popular notations, it is much more consistent with tower notation as a whole. Also, tower notation does not have any ambiguity when compared to Maurer's left-superscript notation, since any multiple like 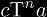$c{\rm T}^na$ is clearly delimited by the T (Greek tau).

Home of Tetration

Towers

Definitions

Notations