
Tetration

As discussed earlier, tetration is the continuously iterated exponential of one. Other names for this operation in the past have been: towers, power towers, plexation, hyper-powers, super-powers, super-exponentiation, the hyper4 operator, iterated exponentials, or iterated exponentiation. The notation for this operation can be any of the notations that can express hyper-operations, because tetration is hyper4, or the left-superscript notation coined by Hans Maurer which was later popularized by Rudy Rucker, or the double-superscript notation that is used on this website.
The defining property of tetration is borrowed from the defining property of hyper-operations. For any extension of tetration to real numbers (continuously iterated exponentials), satisfying this property is essential:
| • |
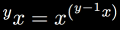
| the defining property of tetration |