About the Definitions

The following definitions are based on widely available definitions, including Munafo's definition of the hyper-operators. The only new definition here is the definition of the super-logarithm, which is discussed in more detail in my paper.

Definitions

Knuth

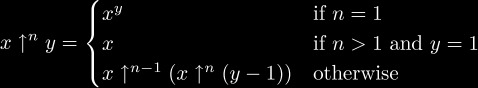
Hyper-operators: $x \uparrow^{n} y = \begin{cases} x^y & \text{if } n = 1\\ x & \text{if } n > 1 \text{ and } y = 1\\ x \uparrow^{n-1} (x \uparrow^{n} (y-1)) & \text{otherwise} \end{cases}$

Exponentiation

This is the usual definition of exponentiation, defined so that integer powers and non-integer powers are, in effect, separate definitions. Since the logarithm has multiple values in the complex plane, it should be understood that only the principle branch of the logarithm is used:

`x`¹ := `x`
`x`ⁿ := `x` `x`^n-1	for integer `n` > 1
`x`^y := e^{y log(x)}	for non-integer `y`

Hyper-operations

This is defined so that the base case of addition is defined, and all hyper-operators after it will have 1 as an identity element. For other values of hyper-operators, see the Identities page. To allow later hyper-operators to be defined in terms of previous hyper-operators, the last part defines hyper-operators recursively:

`x`⁽ⁿ⁾1 := `x`	for integer `n` > 1
`x`⁽¹⁾`y` := `x` + `y`	for integer `y`
`x`⁽ⁿ⁾`y` := `x`^{(n - 1)}(`x`⁽ⁿ⁾(`y` - 1))	for integer `y`, `n` and `n` > 0

Super-logarithms

This definition is different than any other definitions of the super-logarithm. The only place you can find this definition is here, on this website, and in my paper. The first two parts define the super-logarithm everywhere in terms of the interval 0 < z ≤ 1. Once the values are within that interval, the third part uses the series approximation, which converges on that interval:

slog_x(`z`) := slog_x(`x`^z) - 1	if `x` > 1, `z` ≤ 0
slog_x(`z`) := slog_x(log_x(`z`)) + 1	if `x` > 1, `z` > 1
slog_x(`z`) := -1 + ∑ _k=1..∞ `z`^k `s`_k(`x`)	if `x` > 1, 0 < `z` ≤ 1 where `s`_k(`x`) = lim_{n → ∞} det(C_k(`x`)_n)/ det(C₀(`x`)_n) and (C_m(`x`)_n)_jk = ( k^(j−1) - δ_(j−1)k `k`! log(`x`)^(1−j) ) (1 - δ_mk) + δ_mk where `j`,`k` = 1..`m` and δ_mk is Kronecker delta.

Tetration

This defines tetration completely in terms of the super-logarithm, but because the range of the super-logarithm never goes below -2, the first part defines tetration recursively until y > -2. Once it is, then y will be within the proper interval for the second part. The reason why neither of the intervals includes -2, is because tetration is undefined at y = -2. Furthermore, tetration is undefined at every negative integer except -1.

^yx := log_x(^y+1x)

if x > 1, y < -2

^yx := slog_{_x
-1}(y)

if x > 1, y > -2

Continuously Iterated Exponentials

Although it is easy to recognize that tetration (2 arguments) can be defined in terms of iterated exponentiation (3 arguments) where the main input is 1, an interesting relationship allows iterated exponentiation (3 arguments) to be defined in terms of tetration (2 arguments) without any loss of information, so this is its most natural definition:

^yx^a := ^{y + slog_x(a)}x

if x > 1