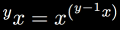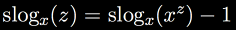Identities
Common Definitions
| |
• nxa =
|

|
for iterated exponentiation
|
| |
• nx =
|

|
for integer tetration
|
Simple Definitions
- nxa = expnx(a)
|
for iterated exponentiation
|
- nx = nx1
|
for integer tetration
|
Inverse Function Formulas
- z = yx
|
tetration
|
- y = slogx(z)
|
super-logarithm
|
- x = srty(z)
|
super-root
|
- z = yxa
|
iterated exponentiation
|
- y = slogx(z) − slogx(a)
|
inverse iterated exponentiation with respect to y
|
- x = srt_(y + slogx(a))(z)
|
inverse iterated exponentiation with respect to x
|
- a = −yxz
|
inverse iterated exponentiation with respect to a
|
Integer Values of Tetration
- −nx
|
undefined for integer n
|
- −2x = ±∞
|
|
- −1x = 0
|
|
- 0x = 1
|
|
- 1x = x
|
|
- 2x = xx
|
|
- ∞x = −W(−log(z)) / log(z)
|
in terms of the product-logarithm, the Lambert-W function.
|
- −∞x = ∞x
|
is a different branch of the infinite iterated exponential.
|
Integer Values of Iterated Exponentiation
- −nxa =
lognx(a)
|
|
- −2xa = logx(logx(a))
|
|
- −1xa = logx(a)
|
|
- 0xa = a
|
|
- 1xa = xa
|
|
- 2xa = x^x^a
|
the graph of which made this website's logo
|
- nxa = expnx(a)
|
|
- ∞xa = ∞x
|
in terms of the infinite iterated exponential.
|
- −∞xa = ∞x
|
is a different branch of the infinite iterated exponential.
|
The Infinite Iterated Exponential and Company
This table shows an interesting relationship:
that these functions are so similar, they can all be expressed in terms of each other.
| |
• ∞x
|
|
= −W(−log(z)) / log(z)
|
|
= 1 / srt2(1 / x)
|
the infinite iterated exponential
|
| |
• ∞(e−x)x
|
|
= W(x)
|
|
= x / srt2(ex)
|
the product-logarithm
|
| |
• 1 / ∞(1 / x)
|
|
= log(z) / W(log(z))
|
|
= srt2(x)
|
the square super-root
|
General Piecewise-Definitions
For tetration:
- yx = logx(y+1x)
|
if y < -1, note: this piece iterates!
|
- yx = t(x, y)
|
if -1 < y ≤ 0
|
- yx = x^(y−1x)
|
if y > 0, note: this piece iterates!
|
where
t(
x,
y) is the
critical function for tetration.
For the super-logarithm:
- slogx(z) =
slogx(xz) − 1
|
if z ≤ 0
|
- slogx(z) = s(x, z)
|
if 0 < z ≤ 1
|
- slogx(z) =
slogx(logx(z)) + 1
|
if z > 1, note: this piece iterates!
|
where
s(
x,
z) is the
critical function for the super-logarithm.
A Simple Extension to Real Numbers
The simplest extension to real numbers is the bare minimum required
to obey the known integer values for tetration and the super-logarithm:
- t(x, y) = y + 1
|
if -1 < y ≤ 0, for tetration
|
- s(x, z) = z − 1
|
if 0 < z ≤ 1, for superlog
|
which satisfy the constraints:
- t(x, -1) = 0
|
like -1x = 0
|
- t(x, 0) = 1
|
like 0x = 1
|
and
- s(x, 0) = -1
|
like slogx(0) = -1
|
- s(x, 1) = 0
|
like slogx(1) = 0
|
Complex Conjugate Properties
Using my extension, these have been verified numerically
for inputs with small imaginary parts between −1/2 and 1/2.
- conj(yx) = conj(y)x
|
for tetration
|
- conj(slogx(z)) = slogx(conj(z))
|
for superlog
|
Integration Formulas
- ∫ x=0..1 xx dx =
∑ n=1..∞ (−1)n+1 / nn
|
Power Tower
Formula #27 -- From MathWorld
|
- ∫ x=0..1 x−x dx =
∑ n=1..∞ 1 / nn
|
Power Tower
Formula #29 -- From MathWorld
|
Hyper-operator Notation
- x(n)y
|
Munafo's hyper-operator notation (de facto standard)
|
- x(n)y = x↑(n−2) y
|
Knuth's extended up-arrow notation (acedemic standard)
|
- x(n)y = x → y → (n − 2)
|
Conway's chained-arrow notation
|
- x(n)y = { x, y, n }
|
Bower's array notation
|
- x(n)y = hyper(x, n, y)
|
The hyper() function notation
|
- x(n)y = hyper-n(x, y)
|
The hyper-n() function notation
|
Tetration Notation
- yx = "
x^^y"
|
ASCII notation for tetration
|
- yx = x↑↑y
|
Knuth's up-arrow notation
|
- yx = x↑2 y
|
Knuth's extended up-arrow notation
|
- yx = x → y → 2
|
Conway's chained-arrow notation
|
- yx = x(4)y
|
Munafo's hyper-operator notation (de facto standard)
|
- yx = hyper(x, 4, y)
|
The hyper() function notation
|
- yx = hyper4(x, y)
|
The hyper-n() function notation
|
- yx = twry(x)
|
A notation for power tower functions
|
- yx = tetx(y)
|
A notation for tetrational functions
|
Iterated Exponentiation Notation
Galidakis uses the notation
y(
x,
a) for iterated exponentiation,
which is beneficial when
a is complicated.
In ASCII, the same can be expressed using the notation "
x^^y@a",
which can be found in several places around the internet. Interestingly,
some have noticed that the notation "
x^^y.a" is equivalent
to the first-degree approximation of tetration, where
y is the integer part and
a is the fractional part of the value being tetrated.
- yxa = "
x^^y@a"
|
ASCII notation for iterated exponentiation
|
- yxa = "
x^^y.a"
|
ASCII notation for approximate iterated exponentiation
|
- yxa = y(x, a)
|
Galidakis' notation for iterated exponentiation
|
- yxa = expyx(a)
|
A functional notation for iterated exponentiation
|
Miscellaneous
- xy = ey log(x)
|
exponentiation in terms of exp and log
|
- xy = 1 + slog_x(y)x
|
exponentiation in terms of tet and slog
|
- xy = 1xy
|
exponentiation in terms of continuously iterated exponentiation
|
- yx = yx1
|
tetration in terms of continuously iterated exponentiation
|
- yxa = y + slog_x(a)x
|
continuously iterated exponentiation in terms of tetration
|