Super-logarithms

Super-logarithms are inverse functions of tetrational functions. Super-logarithms are variously written using the following notations

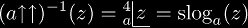
$(a{\U\U})^{-1}(z) = \boxhyperlog{4}{a}{z} = \slog_a(z)$

but on this page, we use the mnemonic notation slog exclusively.

Super-logarithm functions were originally defined over a sparse domain, which consisted of {0, 1, a, a^a, ...} and so on, because these are the only points defined for integer tetration. In order to extend this definition to real numbers or complex numbers, advanced mathematics is required to find a function that satisfies both infinite differentiability and the definition of super-logarithms:

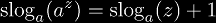
$\slog_a(a^z) = \slog_a(z) + 1$

Power Series

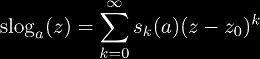
$\slog_a(z) = \sum_{k=0}^{\infty} s_k(a) (z - z_0)^k$

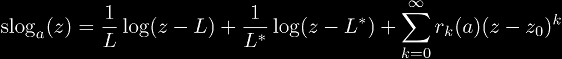
$\slog_a(z) = \frac{1}{L}\log(z - L) + \frac{1}{L^{*}}\log(z - L^{*}) + \sum_{k=0}^{\infty} r_k(a) (z - z_0)^k$

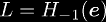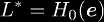where $L = H_{-1}(\ee)$ and $L^{*} = H_{0}(\ee)$ .

Home of Tetration

Super-logarithms

Power Series