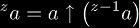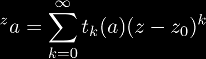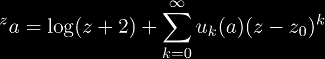Tetrational functions (also called super-exponential functions)
are defined by tetration with a constant base. In other words
the function
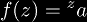 is
a tetrational function. These functions are originally defined
for integer z only, and advanced mathematics is required to find
a function that satisfies infinite differentiability and the definition
is
a tetrational function. These functions are originally defined
for integer z only, and advanced mathematics is required to find
a function that satisfies infinite differentiability and the definition