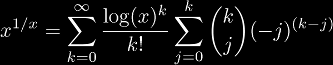Self-root (`x`^1/x)

The self-root function is a simple function related to tetration. It is the inverse function of the infinite tetrate, and thus it corresponds to the infinite super-root.

Series for `x`^1/x

Since x^1/x is such a simple function, we can expand it directly using the series expansion of the exponential function:

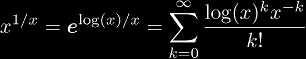
$x^{1/x} = \ee^{\log(x)/x} = \sum_{k=0}^{\infty} \frac{\log(x)^k x^{-k}}{k!}$

The direct function gives the exponential coefficients (1, 1, -2, 3, 4, -90, 786, ...) or (Ax)

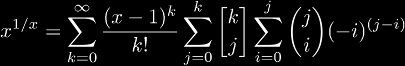
$x^{1/x} = \sum_{k=0}^{\infty}\frac{(x-1)^k}{k!} \sum_{j=0}^{k}\stirfirst{k}{j} \sum_{i=0}^{j}\binom{j}{i}(-i)^{(j-i)}$

If we were to substitute x with e^x expanding about 0 gives the exponential coefficients (1, 1, -1, -2, 9, -4, -95, 414, ...) or (Ax).

$x^{1/x} = \sum_{k=0}^{\infty}\frac{\log(x)^k}{k!} \sum_{j=0}^{k}\binom{k}{j}(-j)^{(k-j)}$

Home of Tetration

Self-root (x1/x)

Series for x1/x

Self-root (`x`^1/x)

Series for `x`^1/x