Lambert W Function

Series for W(x)

Although this is one of the simplest cases of tetration, it is a non-trivial case, since the immediate answer to a series expansion for x^x would be:

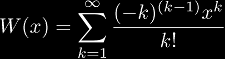
which is not a Taylor series in x. The derivatives of x^x at 1 give the exponential coefficients (1, 1, 2, 3, 8, 10, 54, -42, 944, ...) which is (A005727). In Sloane's database entry for this sequence, Jovovic gives the closed form: showing that a simpler form of the first expansion does exist.